Introduction

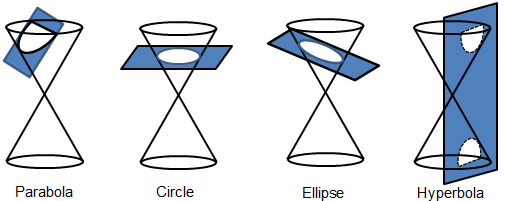
Conic Sections are the figures formed when a plane intersects a double napped right cone. Depending on the angle, the conic section can be a parabola, an ellipse, a circle or a hyperbola.

Double Napped Right Cone, like the one seen in Figure 1, is when two cones opposite to each other and extending infinitely upward and downward. Figure 2 – shows the bottom part of a double napped right cone and how each one of the conic sections are formed.

Figure 2 – The bottom part of a Double Napped Right Cone showing how each one of the conic sections are formed.

 

 

Figure 1 – Double Napped Right Cone showing how each one of the conic sections is formed by cutting at an exact angle.

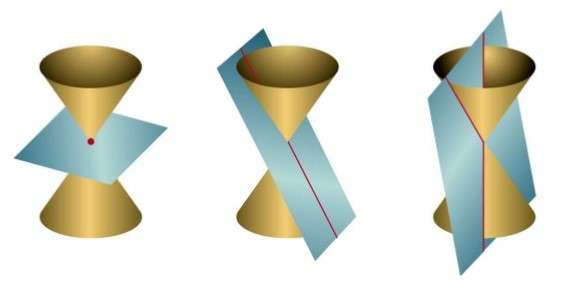
Degenerate Conics form when the plane intersects the vertex of the cone. These include a point, a line or intersecting lines. They do not share the usual properties of conic sections.

A point can only be formed, when a plane passes through the vertex.  A line can only be formed when a plane is tangent to the cone. The intersecting lines are formed when the plane intersects the cone vertically at the middle, like the third cone in Figure 3. Intersecting lines are actually formed by a denegerate hyperbola, which results in two intersecting lines that form an “X”.

Figure 3 – The First double napped right cone shows how a point is formed.The second cone shows the formation of a line. The third cone shows the formation of intersecting lines.

General Form of Equation for Conics

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0

The locus is the set of all points that fulfill a geometric property.